Students use linear models to investigate relationships in demographic data about US states using an inquiry-based approach, involving hypothesizing, experimental and computational modeling, and sense-making.
Lesson Goals |
Students will be able to…
|
Student-facing Lesson Goals |
|
Materials |
|
Supplemental Materials |
|
Key Points For The Facilitator |
|
🔗Looking for Patterns 45 minutes
Overview
Students explore the State Demographics dataset and, building on a discussion of the displays they previously made using the animals dataset, recognize the unique opportunity scatter plots offer for exploring relationships between columns.
Launch
We’re going to search for relationships within a dataset about all the states in the US. But first, let’s take a moment to (1) develop confidence in our ability to use functions for working with tables and making displays, and (2) build familiarity with a new dataset that we are going to spend a lot of time with.
-
Open the Preview: State Demographics Starter File, click "Run", and save a copy of the file.
-
Working in pairs or small groups, complete Exploring the States Dataset.
-
What did you Notice and Wonder?
-
What did you learn about defining rows in Pyret?
-
Example:
x = row-n(states-table, 0)will make the namexhave the value of the first row in the table (the index starts at zero!).
-
-
How would define a name
yto be the value of the second row in the table? The third?-
y = row-n(states-table, 1)for the second row. Change the1to a2for the third.
-
In math, x = 4 will define a variable x to be the value 4.
Any time we see x after that, we can substitute in the value of 4.
This works in Pyret, too. But in Pyret, values can be more than just numbers!
In this file, the variables alabama and alaska are defined as rows from the table.
Debrief the rest of the page with students. Then, initiate a conversation about the various column names, ensuring that students understand all of the terminology. Later in the lesson, students will examine relationships between income and education. We recommend posing the questions below to ensure that they are ready to do so.
-
What columns in this dataset have to do with wealth?
-
pct-in-poverty,poverty-rate,median-income,per-capita-income
-
-
What columns are about education levels?
-
college-or-higher,hs-or-higher
-
Investigate
Before we dig deeper into the State Demographics data, let’s think back to the animals at the shelter in order to introduce some new data science concepts.
-
Does an animal’s age play a role in how long it takes to be adopted? Why or why not?
-
The goal here is to have an open discussion and draw students in. Allow students to share their opinions freely.
-
(For example: Yes, baby animals get adopted quickly because they’re so cute! No, animals require too much work when they are young.)
-
-
What kind of data does the
agevariable represent? What aboutweeks?-
Both
ageandweeksare quantitative variables.
-
-
What kind of display would help us analyze the relationship between age and adoption time?
-
Again, solicit student’s ideas and discuss why each display type would or would not work.
-
Scatter plots reveal the relationship between two columns by plotting one on the x-axis and the other on the y-axis.
Before we can draw a scatter plot, we have to make an important decision: which variable do we think of as the cause - called the explanatory variable - and which is the effect (response variable)?
In this case, which do we suspect is the cause and which is the effect: age or time-to-adoption?
We suspect that age affects the adoption time, so we’ll use age as our explanatory variable and weeks as our response variable. Now our question can be phrased algebraically: is there a function weeks(age) that fits the data?
Why not Independent/Dependent?
When modeling with functions, we typically use terms like dependent variable and independent variable. But even in the presence of a strong correlation, the y-values in a scatter plot are never fully dependent on the x-values. Plenty of scatter plots have no correlation: the y-coordinates do not depend on the x-coordinates at all!
Statisticians commonly use the words explanatory variable and response variable, to more accurately describe the role one column of data plays in explaining another when searching for a relationship.
It’s customary to use the horizontal axis for our explanatory variable and the vertical axis for the response variable. Each row in the dataset will be represented by a point on the scatter plot with age for x and weeks for y.
-
It’s time to dig back into the State Demographics data.
-
Which states do you want to focus on? (Pick our state, a neighboring state, and/or a state you’ve always wanted to visit!)
If students aren’t familiar with neighboring states, here’s a useful map!
Come to a consensus about which states your students will explore. When more students are looking into the same data, you’ll find much richer class discussions!
-
Working in pairs or small groups, complete Part 1 of Looking for Patterns using Preview: State Demographics Starter File.
-
Do not go on to Part 2! We’ll return to that later in the lesson.
Encourage students to first think about which columns might be related, and then create the scatter plot to search for this relationship, rather than making scatter plots for random pairs of columns. The dataset is designed so that students will quickly begin searching for relationships between varying levels of education and income, and there are linear relationships in each of these.
Exploring the States Dataset
The Preview: State Demographics Starter File has a lot of interesting data, and endless possible combinations of columns to explore. But randomly smashing columns together in a scatter plot is not the habit we want students to cultivate! Instead, make sure students are actually talking with their partners about why two columns may or may not be related.
Making sense: can students predict these relationships, and explain their thinking?
(If so, probably not worth having them spend time on more than one of them!)
-
pop-2010vs.pop-2020. -
pop-2020vs.num-households -
num-housing-unitsvs.num-households -
num-householdsvs.num-veterans
Surprises in the District of Columbia: DC often shows up as an outlier or extreme value. But why? Here are a few relationships to spark students' interest.
-
pct-college-or-highervs.pct-in-poverty -
median-incomevs.pct-college-or-higher -
median-incomevs.pct-home-owners -
pct-college-or-highervs.pct-home-owners -
pct-college-or-highervs.pct-home-owners -
pct-home-owners,num-housing-units -
median-incomevs.per-capita-income
Synthesize
-
Share your scatter plots with one another. (Perhaps by copying and pasting
scatter-plotdisplays into a shared document and then labeling those displays?) -
What possible relationships did you find?
-
What did you learn about the state(s) you decided to focus on?
-
Did you and your classmates use similar words to describe the scatter plots you came up with? If so, what were they?
Note: Students will acquire the formal vocabulary that data scientists use to assess relationships in the next section of this lesson, which is all about identifying form, direction, and strength.
🔗Describing Patterns 45 minutes
Overview
Students identify and make use of correlations in scatter plots. They learn to characterize their form as being linear, curved, or showing no clear pattern. They learn that linear patterns have direction, and they learn how to report strength (as well as direction) with a number called the "correlation."
Launch
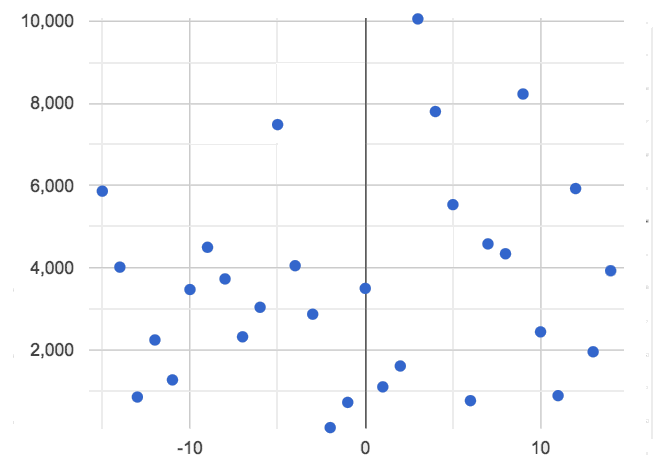
Scatter plots let us visualize the relationship between two quantitative columns. If no relationship exists, the points in the scatter plot just appear as a shapeless cloud. But if there is a relationship, the points will form some kind of pattern. When we build scatter plots, we are searching for patterns between two quantitative variables.
These patterns can be described by three terms: form, direction and strength.
Form
|
|
|
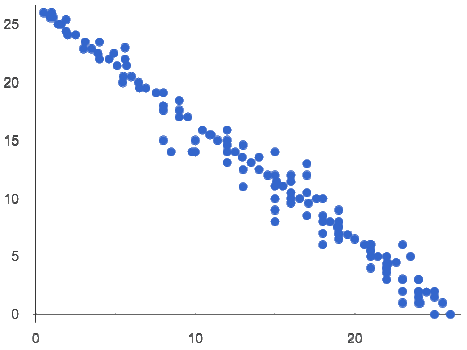
Some patterns appear linear, and cluster around a straight line sloping up or down. |
Some patterns appear nonlinear, and may look like some kind of curve. |
And sometimes there doesn’t appear to be any relationship or pattern at all! |
Form suggests whether a relationship is linear, nonlinear or undefined.
Have students turn to Linear, Non-linear, or Bust? and decide whether each of the scatter plots could be modeled by a linear relationship, a nonlinear relationship, or that there doesn’t appear to be a pattern.
Direction
If the relationship clusters around a straight line, we can talk about direction.
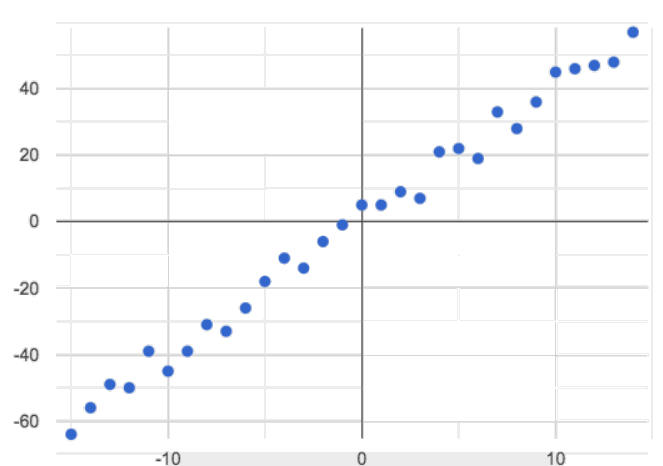 Positive: The line slopes up as we look from left-to-right. Positive relationships are by far the most common because of natural tendencies for variables to increase in tandem. For example, “the older the animal, the more it tends to weigh”.
Positive: The line slopes up as we look from left-to-right. Positive relationships are by far the most common because of natural tendencies for variables to increase in tandem. For example, “the older the animal, the more it tends to weigh”.
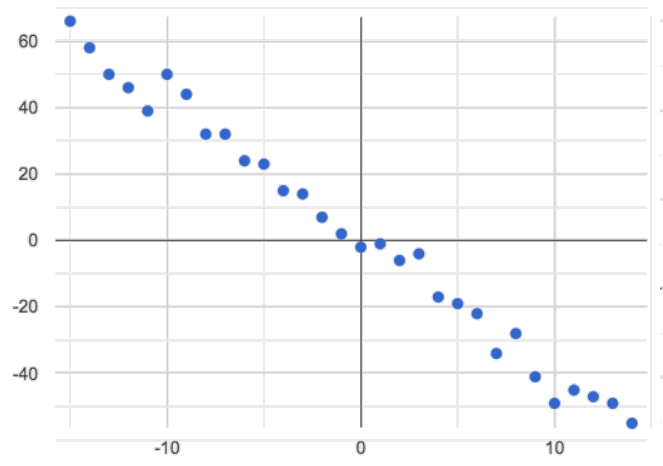 Negative: The line slopes down as we look from left-to-right. For example, “the older a child gets, the fewer new words they learn each day.”
Negative: The line slopes down as we look from left-to-right. For example, “the older a child gets, the fewer new words they learn each day.”
Only linear relationships have direction.
Not every shape has a direction! For example, a curve can start out sloping upwards, but then peak and slope downwards.
Strength
Strength indicates how closely the two variables are related.
 A relationship is strong if knowing a data point’s x-value gives us a very good idea of what its y-value will be (knowing a student’s age gives us a very good idea of what grade they’re in). A strong linear relationship means that the points in the scatter plot are all clustered tightly around an invisible line.
A relationship is strong if knowing a data point’s x-value gives us a very good idea of what its y-value will be (knowing a student’s age gives us a very good idea of what grade they’re in). A strong linear relationship means that the points in the scatter plot are all clustered tightly around an invisible line.
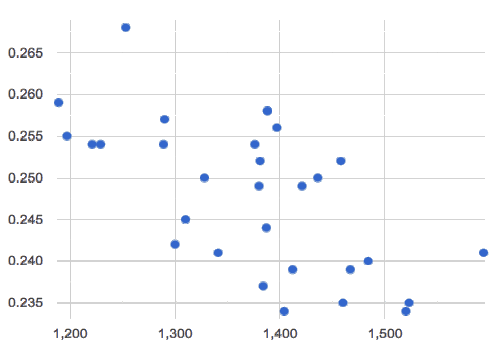 A relationship is weak if x tells us little about y (a student’s age doesn’t tell us much about their number of siblings). A weak linear relationship means that the cloud of points is scattered very loosely around the line.
A relationship is weak if x tells us little about y (a student’s age doesn’t tell us much about their number of siblings). A weak linear relationship means that the cloud of points is scattered very loosely around the line.
Investigate
Now that you’ve dug into the role that form, direction and strength play in assessing a relationship between two quantitative variables, it’s time to put those concepts to work!
-
We need to train our eyes to look for form so that we know whether we’re justified in fitting a line to the scatter plot and reporting a correlation, neither of which would be appropriate if the form is non-linear.
-
Let’s start by practicing matching scatter plots to their descriptions on Identifying Form, Direction and Strength (Matching).
-
Then turn to Identifying Form, Direction and Strength and work with your partner or group to describe each scatter plot.
-
You may want to review the matching answers before having students complete the second page.
-
For students who are struggling, hearing what their peers are looking for is especially helpful at this stage, so be sure to have students explain their thinking for these activities.
-
Some of the answers are not so clear-cut, and students may disagree about what constitutes a "strong" vs. "weak" correlation. We’ve tried to choose scatter plots that clearly fall into one category or the other, but without diving into the algorithm for linear regression students may find this exercise somewhat subjective… and that’s ok!
Return to Looking for Patterns, and apply what you’ve learned about Form, Direction and Strength to complete Part 2.
Common Misconceptions
-
Students often conflate strength and direction, thinking that a strong correlation must be positive and a weak one must be negative.
-
Students may also falsely believe that there is ALWAYS a correlation between any two variables in their dataset.
-
Students often believe that strength and sample size are interchangeable, leading to mistaken assumptions like "any correlation found in a million data points must be strong!" Or "there are only a few data points, so the relationship must be weak!" (Sample size only plays a role if we’re trying to generalize to what’s true for a larger population.)
Synthesize
-
What relationships did you explore in the states dataset?
-
Which appeared to have strong correlations? Were they positive or negative?
-
Were any of these relationships a surprise? Why or why not?
🔗Building Linear Models 45 minutes
Overview
Building on prior knowledge of linear functions, students learn to find the line of best fit to model the relationship in a scatter plot that looks linear. This yields a predictor function that tells what y-value to expect for a given x-value. Students also learn how to quantify how closely a model fits a dataset, using residuals and S as a measure of how well their models fit the data.
Launch
Before we learn to fit linear models to scatter plots, let’s review. What do you remember about linear functions?
We’d expect students to be able to surface much of the following:
-
Linear functions look like straight lines.
-
Vertical lines are not functions, because their slope is undefined as a result of their horizontal change being zero.
-
The steepness of a line can be described by its slope (or constant rate of change).
-
The slope can be calculated from any two points.
-
Students may remember the slope as $$\displaystyle \frac{change \; in \; y}{change \; in \; x}$$ or $$\displaystyle {rise}\over\displaystyle{run}$$ or $$\displaystyle \frac{y_2 - y_1}{x_2 - x_1}$$.
-
The point where the line crosses the y-axis is called the y-intercept or vertical shift.
-
The x-coordinate of the y-intercept always starts with zero, e.g. (0, y).
-
Diagonal lines have both a y-intercept and an x-intercept.
-
Horizontal lines have a constant rate of change of zero.
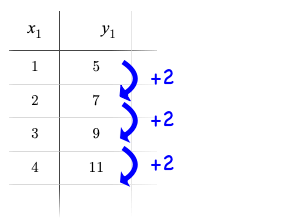 Linear relationships grow by fixed amounts, meaning that the difference between two y-values will always be the same over identical horizontal intervals. In the table shown to the right, you can see arrows pointing out the "jumps" between y-values for intervals of 1. Each jump is the same size.
Linear relationships grow by fixed amounts, meaning that the difference between two y-values will always be the same over identical horizontal intervals. In the table shown to the right, you can see arrows pointing out the "jumps" between y-values for intervals of 1. Each jump is the same size.
If the rate of change is constant, the relationship is linear.
-
Try comparing intervals of 2, instead of intervals of 1.
-
Is the difference between y-values from x = 1 to x = 3 the same as the difference between y-values from x = 2 to x = 4?
-
Yes. When x increases by 2, y increases by 4.
-
Students are about to be asked to write the Slope-Intercept form of the line, given two points in our states dataset. If your students haven’t done much work with calculating slope and y-intercept from pairs of points recently, we recommend prepping them for success by having them complete Defining a Linear Function from Two Points.
Investigate
-
Return to Pyret and the Preview: State Demographics Starter File.
-
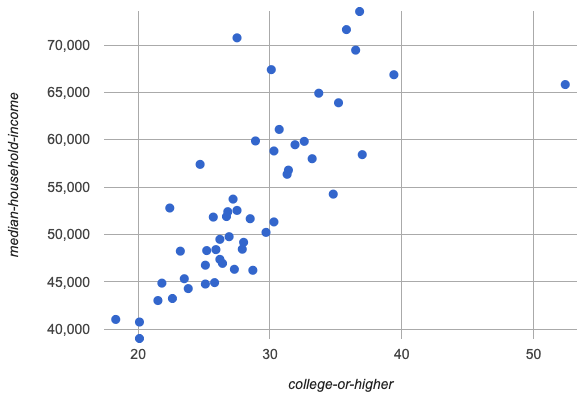
Make a scatter plot showing the relationship between
pct-college-or-higherandmedian-income, usingstatefor the labels.
-
What do you notice about the Form of this scatter plot? What pattern do you see?
-
This scatter plot appears to show a positive, linear relationship:
States with higher percentages of college graduates tend to have higher median household incomes.
-
Suppose the United States were to add a new state.
Based on the data for the existing 50 states (plus DC!)…
-
What median household income would you predict, if exactly 30% of the new state’s citizens had attended college?
-
Answers will vary. But should be above 50,000 and below 60,000
-
-
What would you predict if 20% had attended college?
-
Answers will vary. But should be around 40,000
-
-
If 40% had attended college?
-
Answers will vary. But should be upwards of 65,000
-
 Let students discuss, and explain their thinking.
Let students discuss, and explain their thinking.
-
If possible, mark off a single point for each of the hypothetical percentages, then connect those points to show a straight line.
-
Note that some of these new points would require changing the x-min, x-max, y-min and/or y-max of our display, which we can do by typing in the cells on the right side of the scatter plot and clicking "Redraw".
When we see patterns in data, we can use those patterns to make predictions. We can even draw a line to show all the possible predictions at once! This line is our model of what we think is the underlying relationship.
Now our question can be phrased algebraically! We’re looking for a function that will model the relationship between college enrollment and income, so we want to know if there are values of m and b that will let this function fit the data well:
median-income(pct-college) = m × pct-college + b
If your students could use more support for finding the equation of the line between two points, direct them to the scaffolded version of Build a Model from Samples: College Degrees v. Income (Scaffolded) instead.
Synthesize
Confirm that students were able to successfully compute slope and y-intercept, define and test al-ak(x) in Pyret, and test how well al-ak(x) predicted several states' median income given the percentage of the population with at least a college degree.
-
Why wasn’t the Alaska-Alabama model a good fit for the rest of the data?
-
Because Alaska is an outlier that falls pretty far above the line of best fit.
-
-
If we had chosen two other points from which to build our model, could we have done better? Which points did you choose, and why?
-
Answers will vary. But West Virginia and Massachusetts could be a good option.
-
Write those two states somewhere on Build a Model from Samples: College Degrees v. Income. You’ll want to remember them for later!
🔗Fitting Linear Models 45 minutes
Overview
Students confront the notion of "model fitness". How do we measure how well a model fits? How do we determine which of two models is best? First they’ll consider two models for a simple dataset and brainstorm how we could measure which fits better. Then they’ll test out their linear models using a new pyret function called fit-model, which draws the residuals and computes the Standard Deviation of the Residuals (S).
Launch
In the previous section, we came up with a linear model for the relationship between pct-college-or-higher and median-income, but it definitely wasn’t the best model.
How do we even measure how good a model is?
-
With your partner, complete How could we Measure Whether a Model is a Good Fit?
-
What criteria did you come up with for how to assess whether or not a model is a good fit for the data?
-
Answers will vary. Ideas might include:
-
The points should be as evenly distributed around the model as possible.
-
We could see how the number of points above the line and below the line compare.
-
We could measure the distance between the points and the line and try to make sure the average distance above is balanced with the average distance below.
-
-
-
How could we measure the distance between the data points and the linear model?
-
Answers will vary. Ideas might include:
-
By drawing vertical lines connecting each data points to the linear model.
-
By drawing horizontal lines connecting each data points to the linear model.
-
By drawing diagonal lines connecting each data points to the linear model.
Push students to recognize that in order for this measurement to be useful they would have to be perpendicular to the linear model! -
By drawing squares with one corner on the data point and the opposite corner on the linear model.
-
Pyret has a special function called fit-model that graphs whatever function we give it on top of a scatter plot of the dataset!
-
Take a look at the contract for
fit-modelin your contracts page.
What is its Domain?-
Like
scatter-plot, it consumes columns for our labels, our xs, our ys… *additionally, it consumes a function*.
-
-
Open the Cheerios Starter File and click "Run" to test out
fit-modelwith the dataset and functions you were just looking at. -
What do you Notice? What do you Wonder?
|
|
|
|
 When you graph your model in Pyret, you can see that:
When you graph your model in Pyret, you can see that:
-
some of the points are close to the line ("real" y is close to "predicted" y)
-
some points are quite far away ("real" y is far from "predicted" y)
The difference between any real y and predicted y is called the residual, and it measures how far off that one point in the model is from the actual data.
-
There are three terms in the legend at the bottom. What do they refer to?
-
The blue line is the model.
-
The red dots are the data from the data set.
-
Residuals refer to the vertical black lines connecting the data points to the model, representing the distance between the data and the value the model predicts. They vary in length depending on how far above or below the model the data is situated.
-
-
Compare the
fit-modeldisplay forfto thefit-modeldisplay forg. How are they similar? How are they different?-
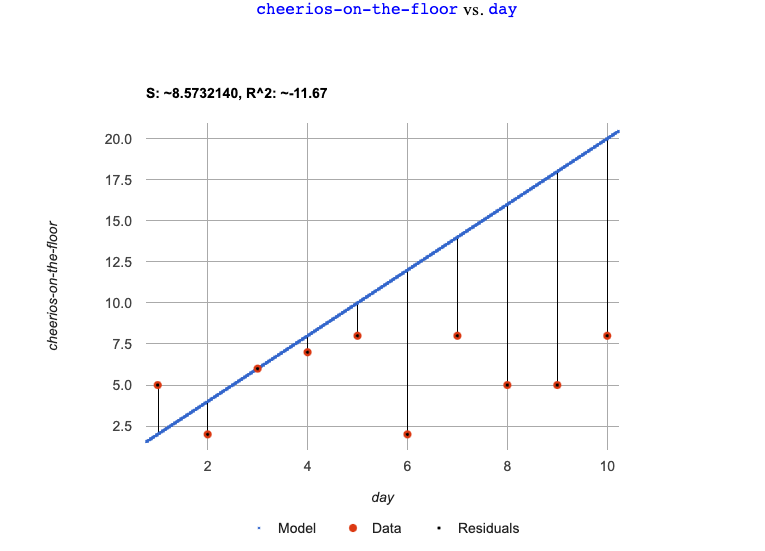
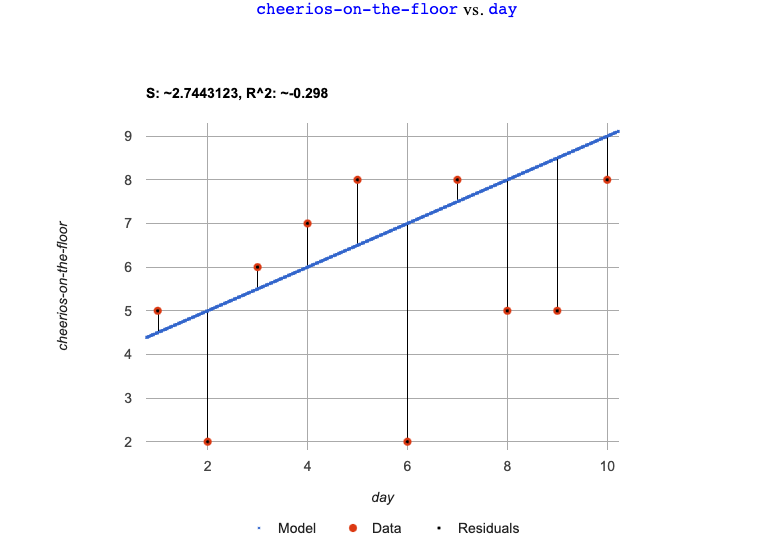
The x-axis goes from 0 to 10 for both of them.
-
The y-axis for
gstops at 9. It goes up to 20 forf. -
Both
fandghave a blue line and red dots. -
fhas significantly more red dots below the blue line than above it. -
The data points for
gmore or less fill the vertical space of the display, whereas forfthere are only data points in the bottom half of the display.
-
There are S and R2 values listed in the top left corner. You probably haven’t seen these terms before, but let’s see if we can figure out what they mean.
-
How do S and R2 compare for the two models?
-
The values are positive for both models and both S and R2 values are smaller for
gthan they are forf.
-
While the remainder of the lesson could be done using the Preview: State Demographics Starter File, you will see us refer to Fitting a Model: State Demographics Starter File from here on out. This file contains the same data, but the Definitions Area is set up to save you time. al-ak has been predefined and the other models students will be asked to define during the remainder of the lesson have been started for them.
Now is the time to make sure students Save a Copy of the file.
-
Open Fitting a Model: State Demographics Starter File and save a copy that’s just for you.
-
Complete Fit a Model: College Degrees v. Income.
Heads up: Sometimes a value has too many digits to be displayed clearly. When this happens, Pyret will convert it to scientific notation. While students in an Algebra 2 class will likely have encountered scientific notation before, they may not recognize 8.23e5 as 8.23 × 105. You should make sure they understand how to interpret this notation.
Pyret has a function that will compute S without drawing the graph. This may be useful, especially for students who are struggling with scientific notation: # S :: (Tablet, Stringlabel, Stringxs, Stringys, Number->Numbermodel) -> Number
-
Based on the S values of the plots you created on this page, what do you think S means?
-
Answers will vary, but students should have some sense of the idea that if one model has a lower S value than another model of the same data it indicates a better fit.
-
There are many different tools to calculate the fitness of a model. You may have heard of R, R2, etc…
Statisticians and Data Scientists are careful to use the right tool for the job!
-
We want a measure of error, so the measure should be zero for a perfect model with no residuals.
-
We want a measure that’s easy to understand, so in our case it should measure how many income-dollars of error a model has.
-
We want a measure that takes the residuals from every data point into account.
S is a measure of fitness, which refers to the Standard Deviation of the Residuals.
-
The closer the data points are to the model, the smaller the residuals are.
-
Smaller residuals mean a smaller S, and a better model!
-
We know that if a model fits the data perfectly, the S value would be 0.
-
Unlike other measures of fitness, S is expressed in terms of units of the y-axis. An S of
2500in this dataset means the standard deviation of the residuals is $2500 - making it much easier to understand.
The S-value always has to be considered in the context of the range of values that the model is predicting!
A model built from Alaska and Alabama predicts that a 1 percent increase in college degrees is associated with a $5613.67 increase in median household income.
-
The lowest median incomes are found in Mississippi ($39.031), Arkansas ($40,768), and West Virginia ($41,043).
-
The highest median income is found in Maryland ($73,538).
With an S-value of 36165, we know that there’s enough error in the model to predict median incomes that are off by $36,165! That’s enough to double the median income of a state or cut it in half!
Compared to the size of the incomes in this dataset, an S value of $36,165 is pretty terrible. This model should not be trusted!
-
Consider the S-value of each model in the context of the range of the data described.
-
Decide how well the model is likely to predict values.
-
Were any of the models described terrific? How do you know?
-
Both 2 and 8
-
Because the numbers in the range were huge and the S value was really small.
-
-
Were any of the models described terrible? How do you know?
-
Both 1 and 6
-
Because the S-value was big in comparison to the range.
-
For the first scenario the S-value was 300, which was the majority of the range between 0 and 400.
-
For the sixth scenario, even though the S-value was only 1, it was much bigger than any of the numbers in the range, which maxed out at two hundredths.
-
-
Complete Graphing Linear Models for a side by side visual comparison of three of your models.
-
What was the best model (lowest S!) you could come up with?
Going Deeper
For a discussion of why the standard error of the regression S may provide more useful information than R2, we recommend visiting this link. Further discussion of S and Residuals may be appropriate for older students, or in an AP Statistics class. We also have an entire Bootstrap:Data Science lesson on Standard Deviation.
Synthesize
-
What does it mean if S is zero?
-
The model fits the data perfectly.
-
-
Is an S-value of 1000 bad?
-
We have no way of knowing out of context! S-values only make sense when considered in the context of the range of the dataset! In our income dataset, 1000 is a pretty good S, because $1000 isn’t a big margin of error. But in a dataset showing the number of students in a school, 1000 would be a very significant error!
-
🔗Finding the Best Linear Model
Overview
Students are introduced to a new pyret function called lr-plot, which uses linear regression to fit the best possible linear model to the data.
Launch
We’ve learned how to measure how well linear models fit the data and to decide which linear model does a better job of predicting values, but how do we find the best possible linear model?
In Statistics, an algorithm called linear regression is used to derive the slope and y-intercept of the best possible model by taking every datapoint into account. Linear regression consumes a dataset and produces a function representing the best linear model.
We could keep guessing and picking two points over and over, and never know if we found the best linear model. Linear regression automatically finds the best-possible model, for any dataset. This is pretty amazing!
Pyret’s lr-plot function finds the best model, and graphs it on top of a scatter plot, and tells us the slope and y-intercept.
More lr-plot material
If you’d like to have students dig deeper into linear regression, there’s an entire lesson you can use that spends more time interpreting results and writing about findings. This lesson also includes a discussion of R2, a different measure of model fitness.
Investigate
-
Turn to Optimizing and Interpreting Linear Models and complete the first section ("Build a Model Computationally").
-
Compare this optimal model to the models you built on Better Modeling: College Degrees v. Income
-
How close did your models come to the optimal model?
-
Did anything about the optimal model surprise you?
Models are only useful if know how to use them!
-
Turn to the second section of Optimizing and Interpreting Linear Models.
-
Using the interpretation of the
al-akmodel you’ll find there as a guide, write up your interpretation of the optimal model you just found for this dataset. Then answer the questions that follow. -
For more practice, build linear models for other relationships in the data. You can use Building More Linear Models.
Optional Activity: Guess the Model!
-
Divide students into teams of 2-4, and have each team come up with a linear, real-world scenario, then have them write down a linear function that fits this scenario on a sticky note. Make sure no one else can see the function!
-
On the board or some flip-chart paper, have each team draw a scatter plot for which their linear function is best fit. They should only draw the point cloud - not the function itself! Finally, students title display to describe their real-world scenario (e.g. - "total cost vs. number of tickets purchased").
-
Have teams switch places or rotate, so that each team is in front of another team’s scatter plot. Have them figure out the original function, write their best guess on a sticky note, and stick it next to the plot.
-
Have teams return to their original scatter plot, and look at the model their colleagues guessed. How close were they? What strategies did the class use to figure out the model?
-
The slope and y-intercepts can be constrained to make the activity easier or harder. For example, limiting these coefficients to whole numbers, positive numbers, etc.
-
To extend the activity, have the teams continue rotating so that each group adds their sticky note for the best-guess model. Then do a gallery walk so that students can reflect: were the models all pretty close? All over the place? Were the guesses for one coefficient grouped more tightly than the guesses for another?
-
Synthesize
-
When does it make sense to make an
lr-plot?-
When we’ve identified that the form of the data is linear
-
-
How could we use scatter plots and linear models to find out if taller NBA players tend to make more three-pointers?
-
How could we use scatter plots and linear models to find out if wealthier people live longer?
-
How could we use scatter plots and linear models to find answers to other questions?
Our model is built from data about all the existing states, which have college attendance rates between 18.3% (West Virginia) and 52.4% (Washington, DC). Suppose two new states were to join the union, one with a 30% college attendance rate and the other with a 90% attendance rate.
Is our model more reliable for one of these states than another? Why or why not?
A model is only as good as the data it was based on. With lots of data between 18.3-52%, this model is much more reliable for the 30% state than the 90% one!
🔗(Optional) Other Forms of Linear Models 45 minutes
Overview
Students are reminded of the three forms of linear models available to us, discuss when and why we might choose one form over another, and practice translating between them.
Launch
When trying to fit a piece into a puzzle, sometimes we rotate the piece to see it from a different angle. When fitting a model to a dataset, we might prefer to look at the linear relationship from different angles as well!
So far we have only discussed vertical shifts, but it is also possible to shift a line or curve horizontally.
The Slope-Intercept form of the line we’ve been using tells us about the slope (m) and the vertical shift. It is also possible to shift a line or curve horizontally, and for some of the non-linear models we will be exploring in this course, identifying the horizontal shift will be important. To prepare ourselves for that thinking, let’s look at how horizontal shifts would fit into our linear model.
Using the form f(x) = m(x - h) + k allows us to change both the horizontal shift (h) and the vertical shift (k).
Note: When the horizontal shift is zero, we can safely remove (h) from the equation. That’s exactly what we’ve been doing with our Slope-Intercept form.
-
Let’s take a moment to explore how horizontal shifts work with linear functions.
-
Complete Exploring Horizontal Shift in Linear Functions (Desmos).
-
Were you able to find any instances where the transformation from a horizontal shift couldn’t be achieved by a vertical shift instead?
-
No. Because lines go on forever without changing direction, horizontal shifts can always be accounted for with vertical shifts. We can prove this to ourselves algebraically because if we distribute the m in the equation f(x) = m(x - h) + k, we get f(x) = mx - mh + k and since mh and k will always be numbers, we can just add them together to get the y-intercept.
-
We will mostly be using Slope-Intercept form of the line in this course, because it’s the simplest form that is defined in terms of the response variable, making it most compatible with the programming environment
But, depending on the information we have available to us - or who we’re writing this model for - we might want to use other forms of linear models. Fortunately, we can always translate any model into another!
You may already be familiar with the different forms of linear models available to us:
| Slope-Intercept | Point-Slope | Standard |
|---|---|---|
y = mx + b |
y - y1 = m(x - x1) |
Ax + By = C |
|
|
|
(1) Slope-Intercept Form makes it really easy to read the slope and y-intercept.
(2) Point-Slope Form makes it easy to find the equation of the line given a single point and slope.
(3) Standard Form makes it easy to find the x- and y-intercepts of the line.
Why do we use these letters as stand-ins for the constants?
The letters used in these forms of the line are just conventions people have agreed upon over time!
Standardized conventions have their benefits, but sometimes they also have downsides.
For example, some students might be confused by the fact that:
-
b in the slope-intercept form and B in standard form represent different things
-
b represents the vertical shift in linear models while it represents the base in exponential models
As we’ve thought through what would best support students with learning to model data, we’ve learned that people are in less agreement about how to name constants for non-linear models.
We believe that what would best support students is to use letters that highlight the similarities between the various models they will be seeing. Our nonlinear modeling materials will consistently use k for the vertical shift.
Applying this to the point-slope form, we’d get: y = mx + k
You can foreshadow this for your students by discussing the fact that while the letters used are conventions, they are stand-ins for patterns and that, having identified the pattern of the point-slope form, we could just as easily have written it with other letters.
Pose the questions below to assess student understanding of when and why we might choose one form over another.
Why we might choose to use one form over another?
-
Suppose our scatter plot has a state with 0% college enrollment, and another with 0% median income. Which linear model form would be easiest to build?
-
Standard Form
-
-
Suppose we only know the slope of a model, but we know the college graduation rate and median income for Rhode Island. Which form would make it easy to figure out the rest of the model?
-
Point-Slope Form
-
-
Which form makes it easiest to define our model in Pyret?
-
Slope-Intercept Form
-
Investigate
While it’s easier to write one linear form or the other based on the information available to us, and might be easier for someone else to extract the information they’re looking for based on the model we supply them with, we can easily translate back and forth between linear forms!
-
Let’s practice writing linear functions in each of the forms and translating them into Pyret function definitions.
-
Turn to Which Form is Best?
-
When you’re done, add your function definitions to your Fitting a Model: State Demographics Starter File and test them out with
fit-model.
Synthesize
If you needed to draw the graph of a linear model, which form would you like to start from? Why?
🔗Additional Exercises
To practice reading linear models and connecting them to graphs:
For practice translating the models we’ve written today into other forms:
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927).  Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.