Correlations

Students identify and make use of patterns in scatter plots, learning to characterize them as being linear, curved, or showing no clear pattern. Determining that a form is linear is a prerequisite for proceeding to correlation and linear regression.

Students have learned several ways to analyze a single quantitative variable, such as age or pounds of the animals in our dataset:

Together, those numbers tell us what value is typical, how much the values vary, and what kind of values are usual or unusual.

But those analyses tell us nothing about the relationship between animals' ages and weights. In order to understand such relationships, we have to expand our view from one column to two. This goes hand-in-hand with expanding our display from a 1-dimensional histogram or box plot to a 2-dimensional scatter plot.

Rather than summarizing each distribution in one dimension, we can search for a linear relationship between two quantitative variables. But linear relationships only make sense if the scatter plot follows a straight-line pattern. So the first thing we need to ask is whether the form of the relationship as being linear or not.

Some patterns are linear, and cluster around a straight line sloping up or down. 🖼Show image

🖼Show imageSome patterns are non-linear, and may look like a curve or an arc.

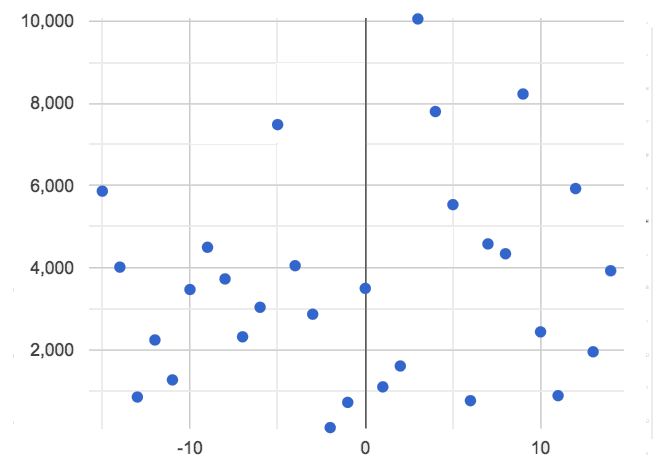🖼Show imageAnd sometimes there is no relationship or pattern at all!

Data Scientists use their eyes all the time! It doesn’t make sense to search for correlations when there’s no pattern at all, and summarizing with a correlation only makes sense for linear relationships!

Once students have learned to identify a possible linear relationship, they can turn their attention to other qualities of that relationship, like its direction.

We can also examine the direction of a linear relationship.

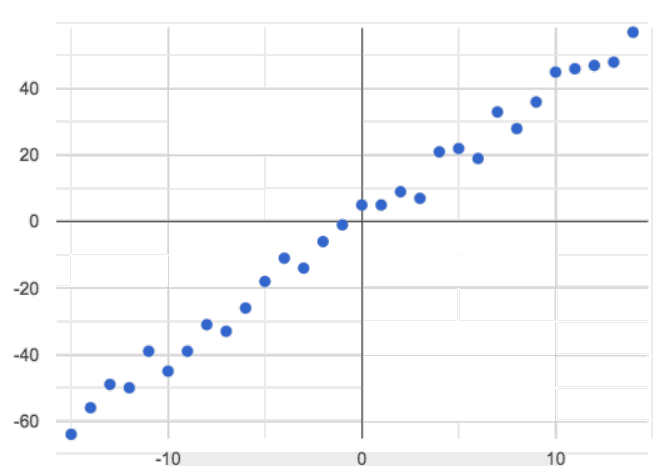🖼Show imagePositive: the line slopes up as we look from left-to-right. Positive relationships are by far most common because of natural tendencies for variables to increase in tandem. For example, “the older the animal, the more it tends to weigh”. This is usually true for human animals, too!

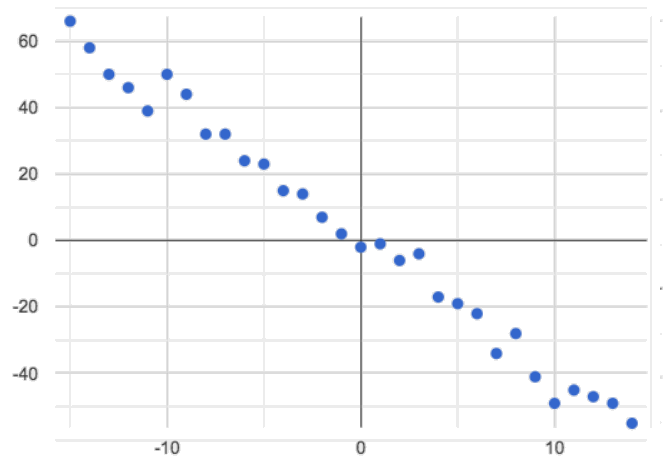🖼Show imageNegative: the line slopes down as we look from left-to-right. Negative relationships can also occur. For example, “the older a child gets, the fewer new words he or she learns each day.”

It only makes sense to look for direction in linear relationships!

Confirm that students have correctly identified the direction of each linear relationship.

We’ll explore another quality of a possible linear relationship: its strength.

Strength indicates how closely the two variables are correlated.

How well does knowing the x-value allow us to predict what the y-value will be?

🖼Show imageA relationship is strong if knowing the x-value of a data point gives us a very good idea of what its y-value will be (knowing a student’s age gives us a very good idea of what grade they’re in). A strong linear relationship means that the points in the scatter plot are all clustered tightly around an invisible line.

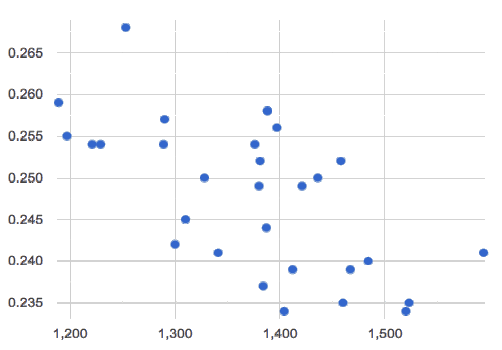🖼Show imageA relationship is weak if x tells us little about y (a student’s age doesn’t tell us much about their number of siblings). A weak linear relationship means that the cloud of points is scattered very loosely around the line.

This page includes a series of probing questions that get at the common misconceptions listed above. Discuss the answers as a class.

If time permits, you might also want to have them complete Identifying Form, Direction and Strength (Matching).

Now that students know how to identify direction and strength for linear relationships, they’ll learn to read how these are expressed in the r$\displaystyle r$-value.

Students have learned that a correlation can be described by three pieces of information: Form, Direction, and Strength. Statisticians and Data Scientists have a shorter way of describing all three, called r-value.

r$\displaystyle r$ is positive or negative depending on whether the correlation is positive or negative. The strength of a correlation is the distance from zero: an r$\displaystyle r$-value of zero means there is no correlation at all, and stronger correlations will be closer to −1 or 1.

An r$\displaystyle r$-value of about ±0.65 or ±0.70 or more is typically considered a strong correlation, and anything between ±0.35 and ±0.65 is “moderately correlated”. Anything less than about ±0.25 or ±0.35 may be considered weak. However, these cutoffs are not an exact science! In some contexts an r$\displaystyle r$-value of ±0.50 might be considered impressively strong!

If it works for you, give students five minutes to play a few rounds of the online game Guess the Correlation to develop intuition with r-values. (This will require creating an account.)

Calculating r$\displaystyle r$ from a dataset only tells us the direction and strength of the relationship in that particular sample. If the correlation between adoption time and age for a representative sample of about 30 shelter animals turns out to be +0.44, the correlation for the larger population of animals will probably be close to that, but certainly not the same.

It’s easy to be seduced by large r$\displaystyle r$-values, and believe that we’re really onto something that will help us claim that one variable really impacts another! But Data Scientists know better than that…​

If time allows, you may want to emphasize the point that correlation does not imply causation by having students look at the nonsense claims that could be made from the graphs of real world data on the Spurious Correlations website.

Which corresponded more strongly with time to adoption, "age" or "pounds"? What does this mean?

The correlation with "pounds" is higher, meaning that an animal’s weight is a better predictor of the number of weeks an animal will live at the shelter before being adopted than its age.

Students repeat the previous activity, this time applying it to their own dataset and interpreting their own results.

Note: this activity can be done as a homework assignment, but we recommend giving students an additional class period to work on this.

What correlations do you think there are in your dataset? Would you like to investigate a grouped sample (subset) of your data to find those correlations?