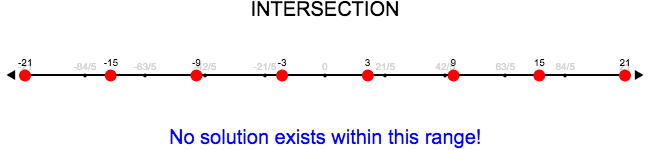Compound Inequalities: Solutions & Non-Solutions

Contribute email twitter instagram facebook

Lessons
Prerequisites for this lesson ★

Standards in this Lesson

Common Core Math Standards

7.EE.B.4: Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
HSF.IF.A.2: Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.
HSS.CP.A.1: Describe events as subsets of a sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions, intersections, or complements of other events ('or', 'and', 'not').

CSTA Standards

3B-AP-10: Use and adapt classic algorithms to solve computational problems.

Oklahoma Standards

OK.6.A.3.1: Represent real-world or mathematical situations using expressions, equations and inequalities involving variables and rational numbers.
OK.7.A.3.3: Represent real-world or mathematical situations using equations and inequalities involving variables and rational numbers.
OK.A1.A.2.2: Represent relationships in various contexts with compound and absolute value inequalities and solve the resulting inequalities by graphing and interpreting the solutions on a number line.
OK.PA.A.4.3: Represent real-world situations using equations and inequalities involving one variable.

Textbook Alignment

IM Algebra 1

IM.Alg1.2.18: Representing Situations with Inequalities

Practices in this Lesson

MP.1: Make sense of problems and persevere in solving them
MLR.5: Co-Craft Questions and Problems

(Also available in WeScheme)

Students build upon their understanding of booleans and simple inequalities to compose compound inequalities using the concepts of union and intersection.

Lesson Goals

Students will be able to:

Understand how the conjunctions and and or differ
Describe how functions can work together
Describe the solution set of a compound inequality

Student-Facing Lesson Goals

I can explain the difference between how and and or are used in programming
I can use two or more inequalities together and describe the area they enclose

Materials

Preparation

Make sure all materials have been gathered
Decide how students will be grouped in pairs

Glossary

function: a mathematical object that consumes inputs and produces an output
intersection: the set of values that makes both inequalities true
union: the set of values that makes either or both of a set of inequalities true

🔗Introducing Compound Inequalities

Overview

Students consider the need to compose inequalities, and think about how to write them.

Launch

We use inequalities for lots of things:

Is it hot out? ( $\displaystyle temperature \gt 80°$ )
Did I get paid enough for painting that fence? ( $\displaystyle paid \ge $100$ )
Are the cookies finished baking? ( $\displaystyle timer = 0$ )

Have students come up with other examples.

Many times we need to combine inequalities:

Should I go to the beach? ( $\displaystyle temperature \gt 80°$ and $\displaystyle weather = "sunny"$ )
Was this burrito worth the price? ( $\displaystyle taste = "delicious"$ and $\displaystyle price \leq $15$ )

Have students come up with other examples.

Guide students through other examples of and and or with various statements, such as "I’m wearing a red shirt AND I’m a math teacher, true or false?" or "I’m an NBA basketball star OR I’m having pizza for lunch, true or false?". This can make for a good sit-down, stand-up activity, where students take turns saying compound boolean statements and everyone stands if that statement is true for them.

Investigate

Both mathematics and programming have ways of combining - or composing - inequalities.

Complete Converting Circles of Evaluation to Code and Compound Inequalities — Practice.

Synthesize

Be really careful to check for understanding here.

Expressions using and only produce true if both of their sub-expressions are true.
Expressions using or produce true if either of their sub-expressions are true.

Strategies for English Language Learners

When describing compound inequalities, be careful not to use "english shortcuts". For example, we might say "I am holding a marker and an eraser" instead of "I am holding a marker and I am holding an eraser." These sentences mean the same thing, but the first one obscures the fact that "and" joins two complete phrases. For ELL/ESL students, this is unecessarily adds to cognitive load!

🔗Solutions and Non-Solutions of Compound Inequalities

Launch

Have students identify 4 solutions and 4 non-solutions for each of the following inequalities.

$\displaystyle x \gt 5$
$\displaystyle x \le 15$

What about the solution set of $\displaystyle x \gt 5$ and $\displaystyle x \le 15$ ? What numbers make both of these inequality expressions true?

How would that be different from $\displaystyle x \gt 5$ or $\displaystyle x \le 15$ ? What numbers make at least one of these inequality expressions true?

Investigate

Have students log in to the Compound Inequalities Starter File (Pyret), read the code carefully and click run to see the graphs they’ve just considered.

This starter file includes two special functions.

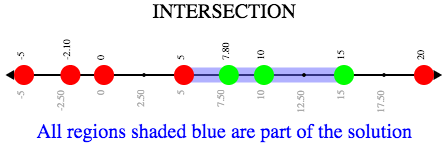
and-intersection takes in two functions and a list of numbers and produces a graph with the points and the shaded intersection of values that make both of the inequalities true.

fun gt5(x): x > 5 end

fun lte15(x): x <= 15 end

and-intersection(gt5, lte15, [list: -5, -2.1, 0, 5, 10, 39/5, 15, 20])

🖼Show image

fun lt5(x): x < 5 end

fun gte15(x): x >= 15 end

and-intersection(lt5, gte15, [list: -5, -2.1, 0, 5, 10, 39/5, 15, 20])

Note: Some pairs of inequalities do not intersect at all and therefore have no solutions.

🖼Show image

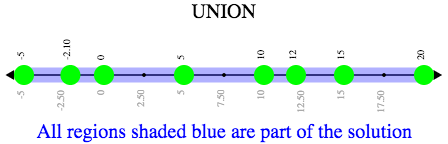
or-union takes in two functions and a list of numbers and produces a graph with the points and the shaded union of values that make either or both of the inequalities true.

fun lt5(x): x < 5 end

fun gte15(x): x >= 15 end

or-union(lt5, gte15, [list: -5, -2.1, 0, 5, 10, 39/5, 15, 20])

🖼Show image

fun gt5(x): x > 5 end

fun lte15(x): x <= 15 end

or-union(gt5, lte15, [list: -5, -2.1, 0, 5, 10, 39/5, 15, 20])

Note: Some unions, like the one below, include all real numbers; they have have infinite solutions that satisfy at least one of the inequalities.

🖼Show image

Turn to Compound Inequalities: Solutions & Non-Solutions and explore the compound inequalities listed using the Compound Inequalities Starter File , identifying solutions and non-solutions for each.

Instead of defining two functions as simple inequalities, we could produce the same graph by defining one function to be a compound inequality.

fun fiveto15(x): (x > 5) and (x <= 15) end inequality(fiveto15, [list: -5, -2.1, 0, 5, 10, 12, 15, 20])

Turn to Compound Inequality Functions and have students write code to describe the compound inequalities pictured.

If you have time, have students open to Matching Compound Inequality Functions and plots (Desmos)

Synthesize

How did the graphs of intersections and unions differ?

🔗Additional Exercises:

Converting Circles of Evaluation with Booleans to Code 2

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, and 1738598). Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.