(Also available in Pyret)
Students learn to model the structure of arithmetic expressions with a visual tool known as "Circles of Evaluation".
Lesson Goals |
Students will be able to:
|
Student-facing Goals |
|
Materials |
|
Supplemental Materials |
|
Preparation |
|
Key Points For The Facilitator |
|
🔗Order of Operations 30 minutes
Overview
Students are given a challenging expression that exposes common misconceptions about order of operations. The goal is to demonstrate that a brittle, fixed notion of order of operations is insufficient, and lead students to a deeper understanding of order of operations as a grammatical device, rather than a computational one. The Circles of Evaluation can be thought of as "sentence diagramming for arithmetic".
Circles of Evaluation
The Circles of Evaluation are a critical pedagogical tool in this course. They place the focus on the structure of mathematical expressions, as a means of combating the harmful student belief that the only thing that matters is the answer.
 The order of operations are often summarized by models like this pyramid or mnemonics like PEMDAS, GEMDAS, etc. These rules are brittle, and don’t always make it clear what we need to do.
The order of operations are often summarized by models like this pyramid or mnemonics like PEMDAS, GEMDAS, etc. These rules are brittle, and don’t always make it clear what we need to do.
Imagine a student with only these tools confronting the expression, $$\displaystyle \frac{7 + 8}{2}$$ or √ - 2
What we need is a better way to read math!
Circles of Evaluation can be used to diagram arithmetic sentences to expose common misconceptions about Order of Operations, and make an excellent scaffold for tracing mistakes when a student applies the Order of Operations incorrectly. They are also a bridge representation, which naturally connects to function composition and converting arithmetic into code.
Launch
If you were to write instructions for getting ready for school, it would matter very much which instruction came first!
Imagine what might happen if someone tried to follow these steps:
-
Put on your sneakers.
-
Tie your sneakers.
-
Put on your socks.
Sometimes we need multiple expressions in mathematics, and the order matters there, too!
Mathematicians didn’t always agree on the Order of Operations, but at some point it became important to establish conventions that would allow them to work together.
This math problem went viral on social media recently, with math teachers arguing about what the answer was!
6 ÷ 2(1 + 2)
-
Take a minute to think about the answer before we learn a new strategy for drawing the structure of this expression so that we can settle the debate!
-
Then turn to Circles of Evaluation - Notice and Wonder and take a minute to record what you Notice and Wonder about the Circles of Evaluation you see.
-
What did you Notice?
-
What did you Wonder?
The rules for drawing Circles of Evaluation are simple:
1) Every Circle must have one - and only one! - function, written at the top.
2) The inputs to the function are written left-to-right, inside the Circle.
3) Circles can contain other Circles.
The Circle of Evaluation for 8 × (7 - 3) is:
-
Let’s draw the Circle of Evaluation for the expression 10 - (5 + 3)
-
What should we do first?
-
It depends! We can either work
-
outside in:
(- 10 ( )) -
or inside out:
( (+ 5 3))
-
-
Either way, we’ll end up with
If it works for you, use this set of cards to have students physically match expressions and Circles of Evaluations.
-
Turn to Matching Expressions to Diagrams and match each expression with its corresponding Circle of Evaluation.
Confirm that students have correctly identified which circle goes with each expression.
-
Turn to Complete the Circles of Evaluation and complete each Circle of Evaluation based on its corresponding expression.
-
Then turn back to Circles of Evaluation - Notice and Wonder and write an expression for each of the Circles of Evaluation.
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
(* 5 6)
|
(* (/ 15 3) 6)
|
(* 5 (- 28 22))
|
(* (/ 15 3) (- 28 22))
|
(* (/ 15 (- 4 1)) 2)
|
5 × 6 |
15 ÷ 3 × 6 |
5 × (28 - 22) |
15 ÷ 3 × (28 - 22) |
15 ÷ (4 - 1) × 2 |
Investigate
Turn to Expressions -> Circles of Evaluation and draw Circles of Evaluation for each of the expressions.
Spend some time ensuring that students have drawn their circles correctly. You may want to have them compare their circles with their partner, others at their table, or against a provided answer key.
Let’s see if we can settle the internet debate about what 6 ÷ 2(1 + 2) evaluates to. Take a minute to draw the Circles of Evaluation. Then evaluate the expression and see what you get.
(* (/ 6 2) (+ 1 2)) |
→ |
(* 3 3) |
→ |
3 × 3 = 9 |
Pedagogy Note
Circles of Evaluation are a great way to get older students to re-engage with (and finally understand) the order of operations while their focus and motivation are on learning to code. Because we recognize this work to be so foundational, and know that some teachers choose to spend a whole week on it, we have developed lots of additional materials to help scaffold and stretch. You will find about 20 additional pages linked in the Additional Exercises section at the the end of this lesson.
Synthesize
-
Is there more than one way to draw the Circle for 1 + 2? If so, is one way more "correct" than the other?
-
Did you always prefer working outside-in to inside-out? Or did different strategies work better for different kinds of problems? Why?
Challenge students to try using the OTHER way to draw the Circle of Evaluation for the next one they draw!
-
Up until now, we didn’t have a visual spatial model for reading arithmetic expressions… How do Circles of Evaluation compare to previous methods you’ve learned for computing what arithmetic expressions evaluate to (PEMDAS, GEMDAS, etc)?
🔗From Circles of Evaluation to Code 25 minutes
Overview
Students learn how to use the Circles of Evaluation to translate arithmetic expressions into code.
Launch
Besides helping us to see the structure of mathematical expressions in order to evaluate them correctly, Circles of Evaluation can also be used to help us write code!
When converting a Circle of Evaluation to code, it’s useful to imagine a "spider" crawling through the circle.
-
The first thing the spider does is enter the circle by crossing over a curved line (an open parenthesis!).
-
She then visits the operation - also called the function - at the top.
-
After that, she crawls from left to right, visiting each of the inputs to the function.
-
Finally, she has to leave the circle by crossing another curved line (a close parenthesis).
Expression |
→ |
3 + 8 |
Circle of Evaluation |
→ |
(+ 3 8) |
Code |
→ |
|
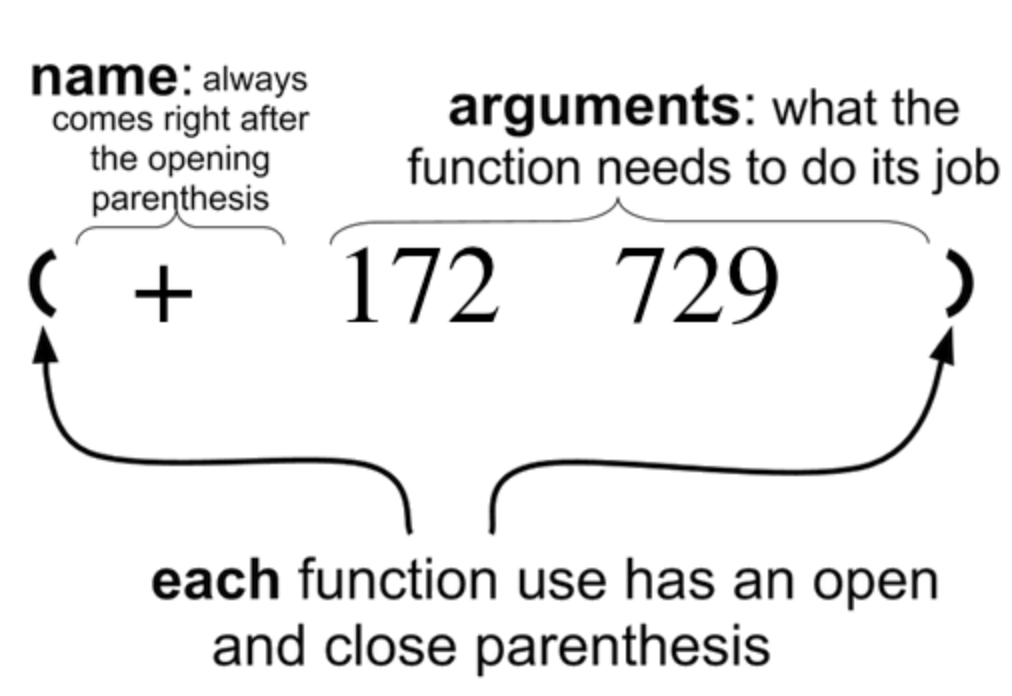
All of the expressions that follow the function name are called arguments to the function. The following diagram summarizes the shape of an expression that uses a function.
Arithmetic expressions involving more than one operation, will end up with more than one circle.
The code for expressions involving more than one operation will have more than one pair of parentheses.
Expression |
→ |
7 + 3 × 2 |
Circle of Evaluation |
→ |
(+ 7 (* 3 2)) |
Code |
→ |
|
-
Why does the code for
(+ 7 (* 3 2))end up with two closing parentheses in a row at the end?-
Because there are two circles that need to be closed!
-
Let’s practice reading Circles of Evaluation for the information we need to write code.
-
Turn to Complete the Code! and fill in the blanks using information from the Circles of Evaluation.
-
Then turn to Complete the Code by adding Parentheses! and add the missing parentheses using information from the Circles of Evaluation.
-
Now that you’ve had a chance to practice, what would the code look like for the expressions represented by these Circles of Evaluation?
(/ 6 (+ 1 2))
|
(* (- 10 5) 6)
|
-
(/ 6 (+ 1 2))(* (- 10 5) 6)
Investigate
On this page, both the Arithmetic Expressions and Circles of Evaluation are provided. Students are just translating them into code. On the next page they will have to draw their own Circles of Evaluation.
Ensure that students have written their code correctly before they move on. You may want to have them compare their code with their partner, or others at their table, before checking against a provided answer key. Ideally, have students do this as they finish rather than trying to keep everybody in sync.
-
Once you confirm that your code is correct, continue on to Expressions -> Circles of Evaluation -> Code 2.
Create space for students to learn at their own speed by directing speedy students to complete Part A of Notice and Wonder - More than +, - , ÷, × from the next lesson section or a page of your choosing from our Additional Exercises.
Strategies For English Language Learners
MLR 7 - Compare and Connect: Gather students' graphic organizers to highlight and analyze a few of them as a class, asking students to compare and connect different representations.
Common Misconceptions
Eagle-eyed students may notice that WeScheme refers to the operator as a function, and ask why it isn’t calling them operators. That’s because operators are functions, and the only reason we use different vocabulary is to highlight the different mathematical grammar (operators go between their arguments, while functions come first). In WeScheme, the notation is the same and so is the vocabulary. This has the added advantage of helping students see the connection between operators and functions.
Synthesize
-
What is something that’s working well for you about using the Circles of Evaluation?
-
What is something that is challenging for you about using the Circles of Evaluation?
-
What questions do you still have about the Circles of Evaluation?
-
If an expression has three sets of parentheses, how many Circles of Evaluation do you expect to need?
🔗Testing out your Code optional
Overview
Circles of Evaluation are a powerful tool that can be used without ever getting students on computers. If you have time to introduce students to the WeScheme, typing their code into the Interactions Area gives students a chance to get feedback on their use of parentheses as well as the satisfaction of seeing their code successfully evaluate the expressions they’ve generated.
Launch
-
Open WeScheme and click "Run".
-
For now, we are only going to be working in the Interactions Area on the right hand side of your screen.
-
Type
(+ (* 8 2) (/ 6 3))into the Interactions Area. -
Notice how the editor highlights pairs of parentheses to help you confirm that you have closed each pair.
-
Hit Enter (or Return) to evaluate this expression. What happens?
-
If you typed the code correctly you’ll get 18.
-
If you make a mistake with your typing, the computer should help you identify your mistake so that you can correct it and try it again!
-
-
Take a few minutes to go back and test each line of code you wrote on the pages you’ve completed by typing them into the Interactions Area. Use the error messages to help you identify any missing characters and edit your code to get it working.
Investigate
Turn to Notice and Wonder - More than +, - , ÷, ×. You will see two Circles of Evaluation at the top. One of them is familiar, but the other is very different from what you’ve been working with. Complete Part A.
(* 10 -4) |
(text "Good work!" 50 "red") |
-
What did you Notice and Wonder?
-
There are more than just operators like addition and subtraction! Math also has functions, and so does Pyret!
-
In math and Pyret, whereas operators like
+,-,*, and/are written in between their inputs, Function names get written at the beginning of an expression, for example(f x)or(sqrt 9). -
When converting a Circle of Evaluation that has a function, the spider starts at the top and visits the function, then visits the inputs from left-to-right.
-
Complete Part B on Notice and Wonder - More than +, - , ÷, ×.
Synthesize
Now that we understand the structure of Circles of Evaluation, we can use them to write code for any function!
-
What are you curious about after what we’ve explored today?
-
What other things could you imagine functions doing?
🔗Additional Exercises
If you are digging into Order or Operations and are looking for more practice with Circles of Evaluation before introducing code, we have lots of options!
More practice connecting Circles of Evaluation to Code
3-column practice connecting Arithmetic Expressions with Circles of Evaluation and Code:
More 3-column practice with negatives:
3-column challenge problems with square roots, brackets, and exponents:
Students must first complete Notice and Wonder - More than +, - , ÷, ×!
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927).  Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.
