instagram

(Also available in Pyret)

Students are introduced to Histograms by comparing them to bar charts, learning to construct them by hand and in the programming environment.

Lesson Goals

Students will be able to…​

  • create histograms using the Animals Dataset

  • create visualizations of frequency using their chosen dataset, and write up their findings

Student-facing Lesson Goals

  • Let’s create histograms for datasets and learn how to interpret them.

Materials

Preparation

🔗Introducing Histograms 20 minutes

Overview

Students look at a bar chart and a histogram, compare/contrast them, and make observations about what they have in common and how they are different. Then they learn a more formal explanation of histograms and practice sketching one by hand.

Launch

Turn to Summarizing Columns with Bar Charts & Histograms, answer the questions about the chart, and identify some ways in which bar charts and histograms are similar and different.

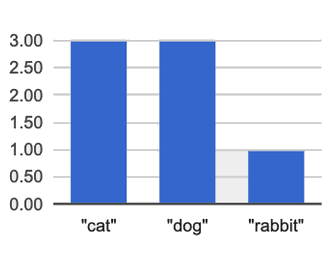bar chart with 3 columns: cat (3), dog (3), rabbit (1). There is a space between each of the bars. The display on the left side of that page is a Bar chart.

  • The x-axis lists the values of a categorical variable (species).

  • The y-axis shows the frequency of categorical values in the dataset.

  • This chart happens to show the categorical values in alphabetical order from left to right, but it would be fine to re-order them anyway we wish. The bar for “dogs” could have been drawn before the one for “cats”, without changing the meaning of the display.

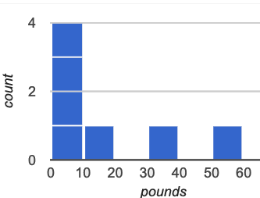bar chart with 3 columns: cat (3), dog (3), rabbit (1). There is a space between each of the bars. The display on the right side is called a histogram.

  • Histograms show the distribution of quantitative data.

  • Since quantitative data must follow a natural order, these bars cannot be re-ordered.

  • Histograms allow us to see the shape of a dataset.

Optional: Kinesthetic Activity

Divide the class into groups of three, and give each group a ball of play-dough. Have the groups roll the dough into a thick cylinder, then divide that cylinder in half. Then, have them take one of the halves and cut that in half again, then cut one of the resulting pieces in half once more. This will form four chunks of play-dough, with a ratio of 1:1:2:4

The play-dough represents a sample, with values falling into four intervals. The largest cylinder represents double the number of "data points" (amounts of dough) as the next largest, which in turn has double the data points of the two small ones.

Histograms pile the data points into equally-sized intervals, just as the cylinders of dough are all of the same width. More dough means longer cylinders, since the "interval width" (cylinder thickness) stays fixed.

Have students line up the cylinders from smallest-to-largest, laying them on a sheet of graph paper. Have them come up with labels for what the x- and y-axis might represent!

Investigate

To build a histogram:

  • Start by sorting all of the numbers in a column from smallest to largest.

  • Mark the x-axis from the smallest value (or a bit below) to the largest value (or a bit above).

  • Divide the x-axis into equally-sized bins (also known as intervals).

    • If our values ranged from 3 to 53 we might mark our x-axis from 0 to 60 and divide it into bins of width 10.

    • If they range from 22 to 41 we might mark our x-axis from 20 to 45 and divide it into bins of width 5.

  • Put each value in our dataset into the bin where it belongs, and then count how many values fall in each bin.

  • The count of the values in each bin determines the height of the bars on our y-axis.

Turn to Making Histograms, and try drawing a histogram from the dataset.

In the histogram we just made,

  • We see that the data is clustered at the right-hand side of the histogram: most people in this sample have close to a full set of teeth, with some people missing a few more than others.

  • Surprisingly, five people have almost no teeth at all! These people are very unusual, and they show up as a small bar far to the left of the main cluster.

Extreme values - which sit far above or below the others - are called outliers

  • Note that intervals on this display include the left endpoint but not the right. If we included the right endpoint and someone had 0 teeth, we’d have to add on a bar from -5 to 0, which would be awfully strange!

Turn to Reading Histograms and practice matching descriptions of video ratings to histograms that could fit the data.

Synthesize

How are histograms and bar charts different?

Want to check student mastery of the content you’ve just taught? Administer Histograms Checkpoint 1 (Desmos) to get a snapshot of your students' current level of mastery. Make sure you have created a link or code for your class to the assessment.

If you’d prefer to wait until your students have completed the entire lesson to check mastery, we also offer a cumulative assessment at the end of Choosing the Right Bin Size, below.

🔗Choosing the Right Bin Size 30 minutes

Overview

Students learn to make histograms from the animals-dataset in Pyret and explore the importance of choosing the right bin size in order for a histogram to show us the shape of the data.

Launch

Bins that are too small will hide the shape of the data by breaking it into too many short bars. Bins that are too large will hide the shape by squeezing the data into just a few tall bars. So far, the bins were provided for you. But how do you choose a good bin-size?

Make sure you have created a link or code for your class to Exploring Bin Size (Desmos).

  • Open the Desmos link I’ve shared with you. (The file should be called Histogram Bin Size Exploration.)

  • Use the Bin Size slider to explore how changing the bin size impacts the shape of the histogram and what we can learn about the distribution of the data.

  • Record your notices and wonders in the space provided on Slide 1.

  • Before moving on to Slide 2, be sure to click the "New Dataset" button and see if you notice and wonder anything new.

  • When you’re done exploring Slide 1, move on to Slide 2 and answer the questions.

Investigate

Suppose we want to know how long it takes for animals from the shelter to be adopted.

Students who haven’t saved this file yet can make a new copy.

  • What did you Notice?

    • We see most of the histogram’s area under the two bars between 0 and 10 weeks, so we can say it was most common for an animal to be adopted in 10 weeks or less.

    • We see a small amount of the histogram’s area trailing out to unusually high values, so we can say that a couple of animals took an unusually long time to be adopted: one took even more than 30 weeks.

    • More than half of the animals (17 out of 31) took just 5 weeks or less to be adopted. But the few unusually long adoption times pulled the average up to 5.8 weeks.

  • What was a typical adoption time?

    • Almost all of the animals were adopted in 10 weeks or less, but a couple of animals took an unusually long time to be adopted — even more than 20 or 30 weeks!

    • Be sure to draw attention to the fact that it would have been hard to give this summary by reading through the table, but the histogram makes it easy to see!

  • What bin sizes worked best for analyzing adoption?

    • Have students talk about the bin sizes they tried. Encourage open discussion as much as possible here, so that students can make their own meaning about bin sizes before moving on to the next point.

Rule of thumb: a histogram should have between 5–10 bins.

Histograms are a powerful way to display a dataset and assess its shape. Choosing the right bin size for a column has a lot to do with how data is distributed between the smallest and largest values in that column! With the right bin size, we can see the shape of a quantitative column.

But how do we talk about or describe that shape, and what does the shape actually tell us?

Our Visualizing the "Shape" of Data lesson addresses these questions…​ and our Measures of Center lesson explores the effect of the shape of a histogram on the mean (average).

Apply what you’ve learned by completing Data Cycle: Shape of the Animals Dataset.

Synthesize

  • What would the histogram look like if most of the animals took more than 20 weeks to be adopted, but a couple of them were adopted in fewer than 5 weeks?

  • What would the histogram look like if every animal was adopted in roughly the same length of time?

Want to check student mastery of the content you’ve just taught? Administer Histograms Checkpoint 2 (Desmos) to get a snapshot of your students' current level of mastery. Make sure you have created a link or code for your class to the assessment.

Alternatively, we offer a compilation of both Checkpoints in Histograms Cumulative Assessment (Desmos).

🔗Data Exploration Project (Histograms) flexible

Overview

Students apply what they have learned about histograms to their chosen dataset. They will add two items to their Data Exploration Project Slide Template: (1) at least two histograms and (2) any interesting questions that emerge.

Visit Project: Dataset Exploration to learn more about the sequence and scope. Teachers with time and interest can build on the exploration by inviting students to take a deep dive into the questions they develop with our Project: Research Capstone.

Launch

Before we shift our focus to your chosen datasets, let’s quickly review what we have learned about making and interpreting histograms.

  • Does a histogram display categorical or quantitative data? How many columns of data does a histogram display?

    • Histograms display a single column of quantitative data.

  • How is a histogram different from a bar chart?

    • Because a bar chart displays categorical data, we can rearrange the bars in any order we wish. Because the quantitative data of a histogram must follow a natural order, bars cannot be rearranged.

  • What do histograms show us about a dataset?

    • Histograms allow us to see the shape of one column of dataset.

  • How can you decide an appropriate bin size for your histogram?

    • A histogram should have 5-10 bins. We want to choose a bin size that lets us the shape of a quantitative column.

Investigate

Let’s connect what we know about histograms to your chosen dataset.

Students have the opportunity to choose a dataset that interests them from our List of Datasets in the Choosing Your Dataset lesson. If you’d prefer to focus your class on a single dataset, we recommend the Global Food Supply & Production Starter File.

  • Open your chosen dataset starter file in CODAP.

  • Choose one quantitative column from your data set that you will represent with a histogram.

  • Create the histogram.

  • What question does your display answer?

    • Possible response: What is the shape of a particular quantitative column of my dataset?

  • Now, write down that question in the top section of Data Cycle: Shape of My Dataset.

  • Then, complete the rest of the data cycle, recording how you considered, analyzed and interpreted the question.

  • Repeat this process for at least one more quantitative column.

Confirm that all students have created and understand how to interpret their histograms.

It’s time to add to your Data Exploration Project Slide Template.

  • Copy/paste at least two histograms. Be sure to also add any interesting questions that you developed while making and thinking about histograms.

You may need to help students locate the “Histogram” slide in the "Making Displays" section. They will need to duplicate the slide to add their second display. The “My Questions” section is at the end of the slide deck._

Note: During the next lesson, Visualizing the "Shape" of Data, students will learn additional vocabulary to help them describe what they see in their histogram. They can add to their histogram interpretations at that point.

Synthesize

Have students share their findings.

  • Did you discover anything surprising or interesting about your dataset?

  • What questions did the bar and pie charts inspire raise?

  • Did other students make any discoveries that were surprising or interesting to you? (For instance: Did everyone find outliers? Was there more or less similarity than expected?)

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.

Lessons

    Aligns to: