Factored Form: y = a(x − r1)(x − r2)

  • a: determines whether the parabola opens up or down and how steep the curve is

  • r1 and r2: roots, x-intercepts

Match each definition below to the graph it describes.

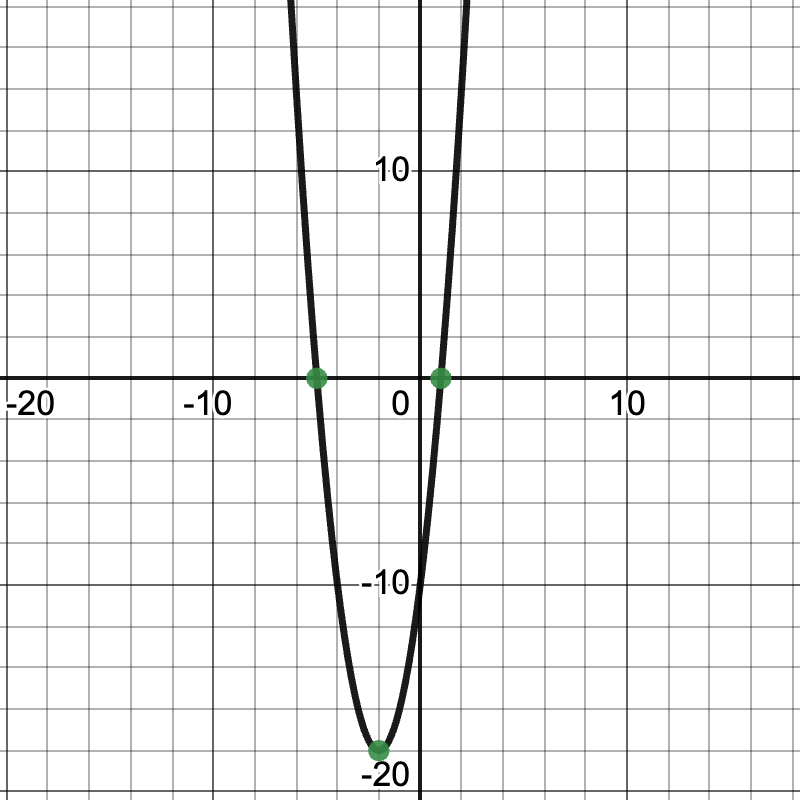
y = 2(x - 1)(x + 5)

1

A

a parabola that opens down, with roots at 1 and 5 and a vertex at (3,12).

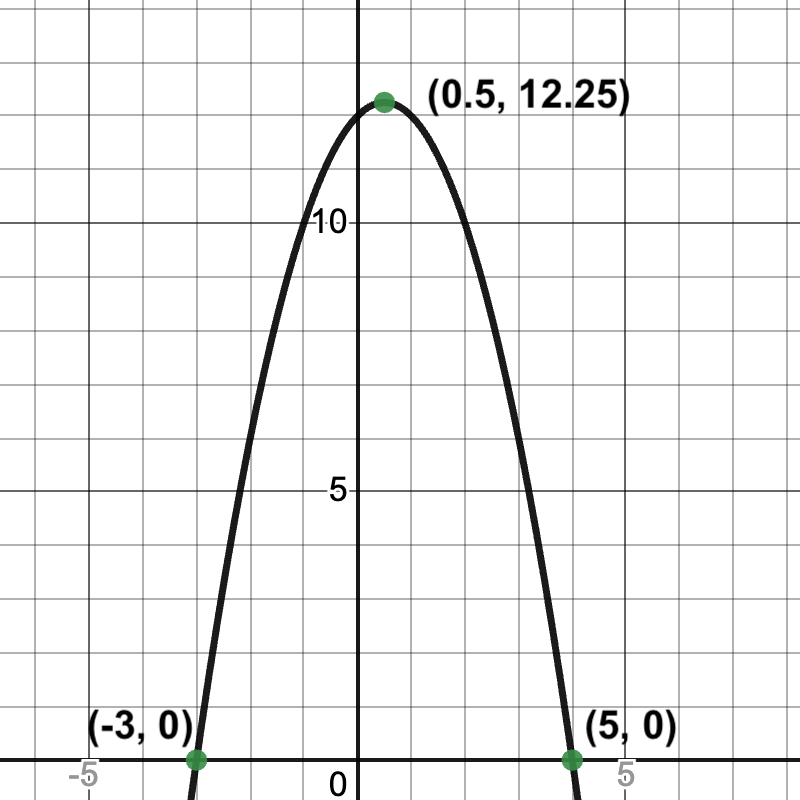
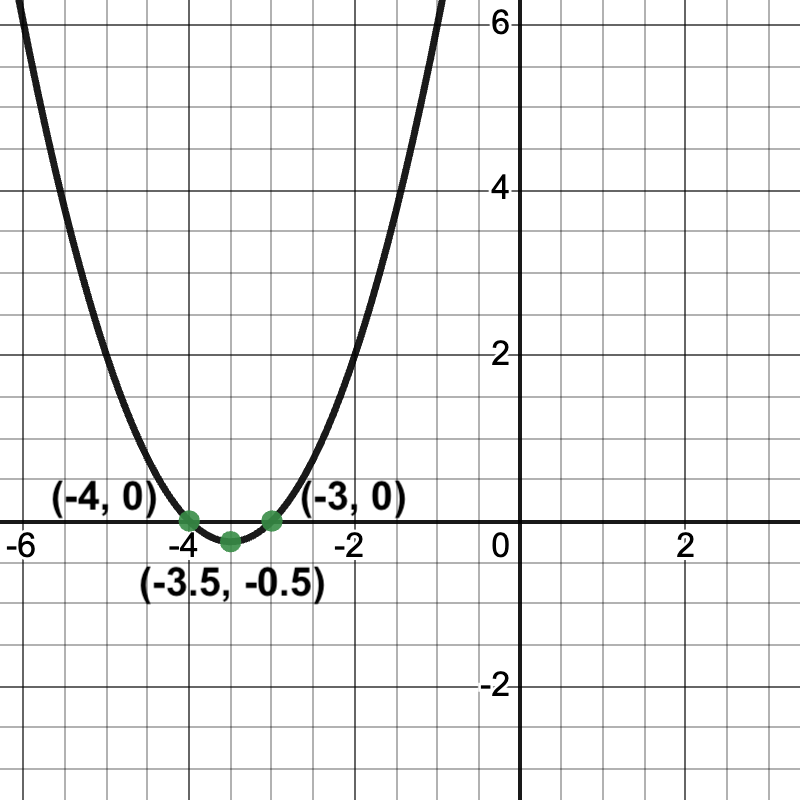
y = (x + 3)(x + 4)

2

B

a parabola that opens down, with roots at -3 and 4 and a vertex at (0.5,12.25).

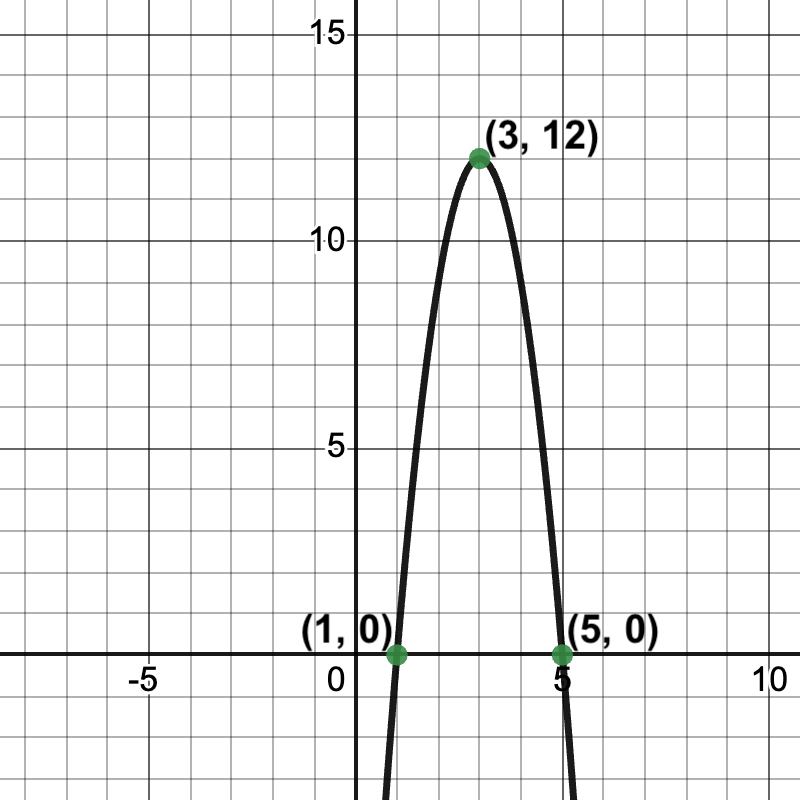
y = - 3(x - 1)(x - 5)

3

C

a parabola that opens up, with roots at -3 and -4 and a vertex at (0.5, 5.125).

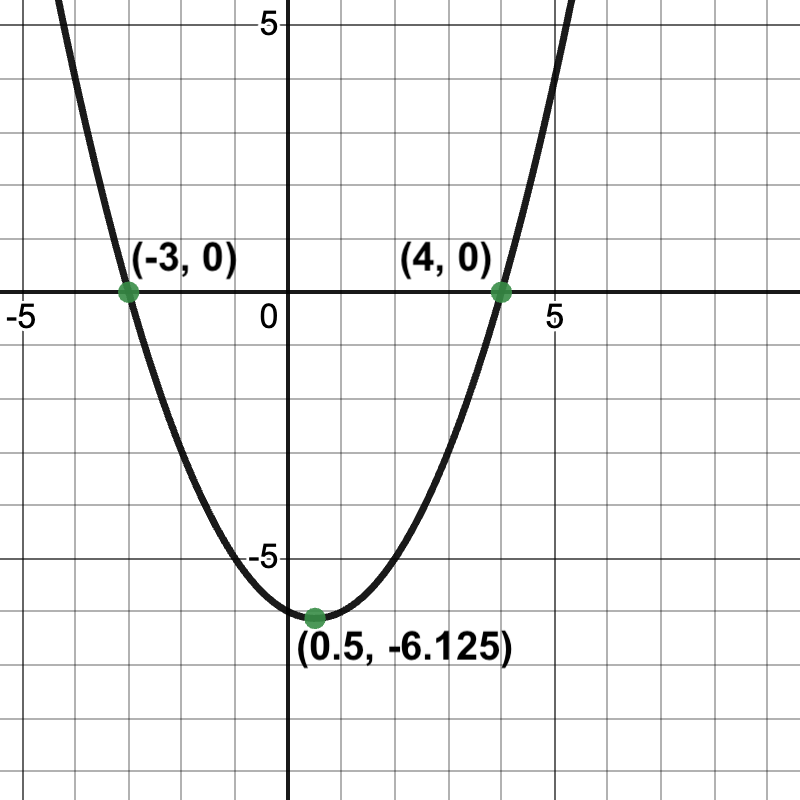
$$\displaystyle y = \frac{1}{2}(x + 3)(x - 4)$$

4

D

a parabola that opens up, with roots at 1 and -5 and a vertex at (-2,18).

y = - (x - 5)(x + 3)

5

E

a parabola that opens up, with roots at -3 and -3 and a vertex at (-3.5, -0.5).

These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). CCbadge Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.