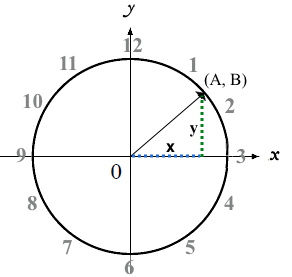
A unit clock (shown below) is centered at the origin (0, 0). As time passes, the point (A, B) rotates around the circle.
1 The radius r of the circle below has a length of 1. What is the length of the hypotenuse of the right-triangle formed by A and B?
|
|
|
2 The tables above show the values of A and B at 12 o’clock. Fill in the values of A and B at 3, 6 and 9 o’clock.
3 In the diagram above, the hand is pointing to (A,B) at 1:30. At this time, A = B. In the space below, (a) draw and label the right triangle, then (2) fill in the remaining blanks in both tables to show A and B.
4 Use the values you computed at 1:30 to fill in the rest of the table with values of A and B at 4:30, 7:30, and 10:30.
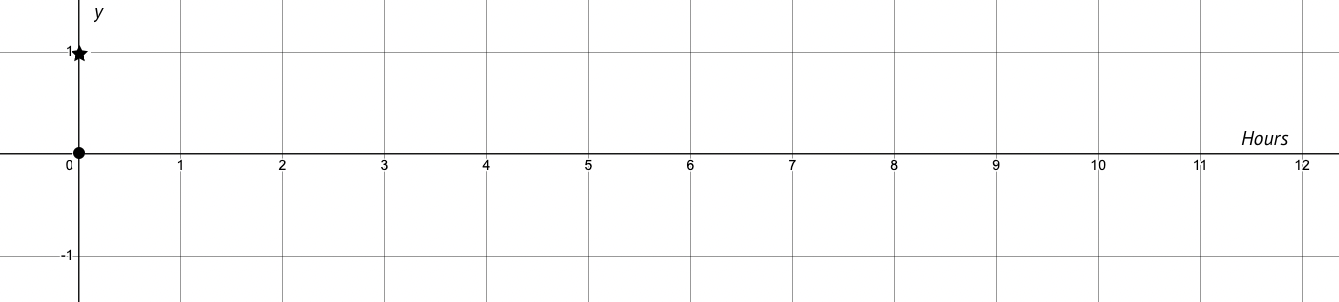
5 In the graph below, draw a dot for the coordinates (time, A) in each row of the table. Connect them from left-to-right, to form a curve.
6 In the graph below, draw a star for the coordinates (time, B) in each row of the table. Connect them from left-to-right, to form a curve.
Open the Desmos File Exploring Periodic Functions. You should be on Slide 1: Unit Clocks.
7 "Turn on" the x(time) folder, and compare the graph to your own graph of A. Do they match?
8 Turn off that first folder, and turn on the one for y(time). Compare the graph to your own graph of B. Do they match?
These materials were developed partly through support of the National Science Foundation, (awards 1042210, 1535276, 1648684, 1738598, 2031479, and 1501927). 
Bootstrap by the Bootstrap Community is licensed under a Creative Commons 4.0 Unported License. This license does not grant permission to run training or professional development. Offering training or professional development with materials substantially derived from Bootstrap must be approved in writing by a Bootstrap Director. Permissions beyond the scope of this license, such as to run training, may be available by contacting contact@BootstrapWorld.org.