
Overview
Students act out a collision in their game, and reason about the mathematical behavior of collision detection
Learning Objectives
Students will be able to explain how a Number line is used to calculate distance in 1 dimension.
Students will be able to explain both conditions used in the line-length function.
Product Outcomes
Standards
Materials
Computers w/ DrRacket or WeScheme
Student workbook
Pens/pencils for the students, fresh whiteboard markers for teachers
Class posters (List of rules, basic skills, course calendar)
Language Table (see below)
Preparation
Suppose two objects are moving through space, each one having it’s own (x,y) coordinates. When do their edges start to overlap? They certainly overlap if their coordinates are identical (x1=x2, y1=y2), but what of their coordinates are separated by a small distance? Just how small does that distance need to be, before their edges touch?
Visual aids are key here - be sure to diagram this on the board!
In one dimension, it’s easy to calculate when two objects overlap. In this example, the red circle has a radius of 1, and the blue circle has a radius of 1.5 The circles will overlap if the distance between their centers is less than the sum of their radii (1+1.5 = 2.5). How is the distance between their centers calculated? In this example, their centers are 3 units apart, because 4-1=3.
Would the distance between them change if the circles swapped places? Why or why not?
Work through a number of examples, using a number line on the board and asking students how they calculate the distance between the points.
Scroll to the line-length and collide? functions in your game files. By making sure to always subtract the smaller coordinate on the number line from the larger one, we can easily find the distance between them. The line-length function does exactly that: it subtracts the smaller number from the bigger one. Can you explain why line-length needs to use Cond? What are the two conditions?
The two conditions are:
A is less than B
B is less than or equal to A
Unfortunately, line-length can only calculate the distance between points in a single dimension (x or y). How would the distance be calculated between objects moving in 2-dimensions? line-length can calculate the vertical and horizontal lines in the graphic shown here, using the distance between the x-coordinates and the distance between the y-coordinates. Unfortunately, it doesn’t tell us how far apart the two centers are.
Drawing a line from the center of one object to the other creates a right-triangle, with sides A, B and C. A and B are the vertical and horizontal distances, with C being the distance between the two coordinates. line-length can be used to calculate A and B, but how can we calculate C?
Students’ gamefiles all have a value called *distances-color*, which is set to the empty string "". By changing this to a color such as "yellow" or "red", the game will draw right triangles between each game character, and fill in the lengths for each side. You may want to demonstrate this using your own game file, and have the students follow along. Hint: to make it as easy as possible to see these triangles, set your background to be a simple, black rectangle and slow down the animation functions.
In a right triangle, the side opposite the 90-degree angle is called the hypoteneuse. Thinking back to our collision detection, we know that the objects will collide if the hypoteneuse is less than the sum of their radii. Knowing the length of the hypoteneuse will be essential to determine when a collision occurs.
 Unit 8
Unit 8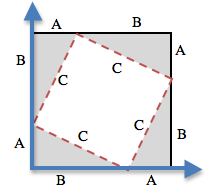 For any right triangle, it is possible to draw a picture where the hypoteneuse is used for all four sides of a square. In the diagram shown here, the white square is surrounded by four gray, identical right-triangles, each with sides A and B. The square itself has four identical sides of length C, which are the hypoteneuses for the triangles. If the area of a square is expressed by , then the area of the white space is
For any right triangle, it is possible to draw a picture where the hypoteneuse is used for all four sides of a square. In the diagram shown here, the white square is surrounded by four gray, identical right-triangles, each with sides A and B. The square itself has four identical sides of length C, which are the hypoteneuses for the triangles. If the area of a square is expressed by , then the area of the white space is  By moving the gray triangles, it is possible to create two rectangles that fit inside the original square. While the space taken up by the triangles has shifted, it hasn’t gotten any bigger or smaller. Likewise, the white space has been broken into two smaller squares, but in total it remains the same size. By using the side-lengths A and B, one can calculate the area of the two squares.
By moving the gray triangles, it is possible to create two rectangles that fit inside the original square. While the space taken up by the triangles has shifted, it hasn’t gotten any bigger or smaller. Likewise, the white space has been broken into two smaller squares, but in total it remains the same size. By using the side-lengths A and B, one can calculate the area of the two squares.
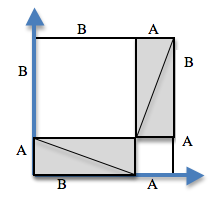 The smaller square has an area of , and the larger square has an area of . Since these squares are just the original square broken up into two pieces, we know that the sum of these areas must be equal to the area of the original square:
The smaller square has an area of , and the larger square has an area of . Since these squares are just the original square broken up into two pieces, we know that the sum of these areas must be equal to the area of the original square: